Replacing the rows of a matrix with corresponding columns is called. Mathematics for dummies. Matrices and basic operations on them. What matrices can be multiplied?

Matrix rows A form line space R(A T).

Matrix columns A form column space matrices and are denoted by R(A).

Kernel or null space of a matrix

The set of all solutions to the equation Ax=0, Where A-m x n-matrix, x- length vector n- forms null space or core matrices A and is denoted by Ker(A) or N(A).

Opposite matrix

For any matrix A there is an opposite matrix -A such that A+(-A)=0. Obviously, as a matrix -A you should take the matrix (-1)A, whose elements differ from the elements A familiar.

Skew-symmetric (skew-symmetric) matrix

A square matrix is ​​called skew-symmetric if it differs from its transposed matrix by a factor of −1:

In a skew-symmetric matrix, any two elements located symmetrically relative to the main diagonal differ from each other by a factor of −1, and the diagonal elements are equal to zero.

An example of a skew-symmetric matrix:

Matrix difference

By difference C two matrices A And B of the same size is determined by the equality

To denote the difference between two matrices, the following notation is used:

Matrix degree

Let a square matrix of size n×n. Then the degree of the matrix is ​​defined as follows:

where E is the identity matrix.

From the associative property of multiplication it follows:

Where p,q- arbitrary non-negative integers.

Symmetric (Symmetric) matrix

Matrix satisfying the condition A=A T is called a symmetric matrix.

For symmetric matrices the equality holds:

a ij =a ji ; i=1,2,...n, j=1,2,...n

DEFINITION OF MATRIX. TYPES OF MATRICES

Matrix of size m× n called a set m·n numbers arranged in a rectangular table of m lines and n columns. This table is usually enclosed in parentheses. For example, the matrix might look like:

For brevity, a matrix can be denoted by a single capital letter, for example, A or IN.

In general, a matrix of size m× n write it like this

.

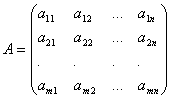The numbers that make up the matrix are called matrix elements. It is convenient to provide matrix elements with two indices a ij: The first indicates the row number and the second indicates the column number. For example, a 23– the element is in the 2nd row, 3rd column.

If a matrix has the same number of rows as the number of columns, then the matrix is ​​called square, and the number of its rows or columns is called in order matrices. In the above examples, the second matrix is ​​square - its order is 3, and the fourth matrix is ​​its order 1.

A matrix in which the number of rows is not equal to the number of columns is called rectangular. In the examples this is the first matrix and the third.

There are also matrices that have only one row or one column.

A matrix with only one row is called matrix - row(or string), and a matrix with only one column matrix - column.

A matrix whose elements are all zero is called null and is denoted by (0), or simply 0. For example,

.

Main diagonal of a square matrix we call the diagonal going from the upper left to the lower right corner.

A square matrix in which all elements below the main diagonal are equal to zero is called triangular matrix.

.

A square matrix in which all elements, except perhaps those on the main diagonal, are equal to zero, is called diagonal matrix. For example, or.

A diagonal matrix in which all diagonal elements are equal to one is called single matrix and is denoted by the letter E. For example, the 3rd order identity matrix has the form .

ACTIONS ON MATRICES

Matrix equality. Two matrices A And B are said to be equal if they have the same number of rows and columns and their corresponding elements are equal a ij = b ij. So if And , That A=B, If a 11 = b 11, a 12 = b 12, a 21 = b 21 And a 22 = b 22.

Transpose. Consider an arbitrary matrix A from m lines and n columns. It can be associated with the following matrix B from n lines and m columns, in which each row is a matrix column A with the same number (hence each column is a row of the matrix A with the same number). So if , That .

This matrix B called transposed matrix A, and the transition from A To B transposition.

Thus, transposition is a reversal of the roles of the rows and columns of a matrix. Matrix transposed to matrix A, usually denoted A T.

Communication between matrix A and its transpose can be written in the form .

For example. Find the matrix transposed of the given one.

Matrix addition. Let the matrices A And B consist of the same number of rows and the same number of columns, i.e. have same sizes. Then in order to add matrices A And B needed for matrix elements A add matrix elements B standing in the same places. Thus, the sum of two matrices A And B called a matrix C, which is determined by the rule, for example,

Examples. Find the sum of matrices:

It is easy to verify that matrix addition obeys the following laws: commutative A+B=B+A and associative ( A+B)+C=A+(B+C).

Multiplying a matrix by a number. To multiply a matrix A per number k every element of the matrix is ​​needed A multiply by this number. Thus, the matrix product A per number k there is a new matrix, which is determined by the rule or .

For any numbers a And b and matrices A And B the following equalities hold:

Examples.

Matrix multiplication. This operation is carried out according to a peculiar law. First of all, we note that the sizes of the factor matrices must be consistent. You can multiply only those matrices in which the number of columns of the first matrix coincides with the number of rows of the second matrix (i.e., the length of the first row is equal to the height of the second column). The work matrices A not a matrix B called the new matrix C=AB, the elements of which are composed as follows:

Thus, for example, to obtain the product (i.e. in the matrix C) element located in the 1st row and 3rd column from 13, you need to take the 1st row in the 1st matrix, the 3rd column in the 2nd, and then multiply the row elements by the corresponding column elements and add the resulting products. And other elements of the product matrix are obtained using a similar product of the rows of the first matrix and the columns of the second matrix.

In general, if we multiply a matrix A = (a ij) size m× n to the matrix B = (b ij) size n× p, then we get the matrix C size m× p, whose elements are calculated as follows: element c ij is obtained as a result of the product of elements i th row of the matrix A to the corresponding elements j th matrix column B and their additions.

From this rule it follows that you can always multiply two square matrices of the same order, and as a result we obtain a square matrix of the same order. In particular, a square matrix can always be multiplied by itself, i.e. square it.

Another important case is the multiplication of a row matrix by a column matrix, and the width of the first must be equal to the height of the second, resulting in a first-order matrix (i.e. one element). Really,

.

Examples.

Thus, these simple examples show that matrices, generally speaking, do not commute with each other, i.e. A∙B ≠ B∙A . Therefore, when multiplying matrices, you need to carefully monitor the order of the factors.

It can be verified that matrix multiplication obeys associative and distributive laws, i.e. (AB)C=A(BC) And (A+B)C=AC+BC.

It is also easy to check that when multiplying a square matrix A to the identity matrix E of the same order we again obtain a matrix A, and AE=EA=A.

The following interesting fact can be noted. As you know, the product of 2 non-zero numbers is not equal to 0. For matrices this may not be the case, i.e. the product of 2 non-zero matrices may turn out to be equal to the zero matrix.

For example, If , That

.

THE CONCEPT OF DETERMINANTS

Let a second-order matrix be given - a square matrix consisting of two rows and two columns .

Second order determinant corresponding to a given matrix is ​​the number obtained as follows: a 11 a 22 – a 12 a 21.

The determinant is indicated by the symbol .

So, in order to find the second-order determinant, you need to subtract the product of the elements along the second diagonal from the product of the elements of the main diagonal.

Examples. Calculate second order determinants.

Similarly, we can consider a third-order matrix and its corresponding determinant.

Third order determinant, corresponding to a given third-order square matrix, is a number denoted and obtained as follows:

.

Thus, this formula gives the expansion of the third-order determinant in terms of the elements of the first row a 11 , a 12 , a 13 and reduces the calculation of the third-order determinant to the calculation of the second-order determinants.

Examples. Calculate the third order determinant.

Similarly, we can introduce the concepts of determinants of the fourth, fifth, etc. orders, lowering their order by expanding into the elements of the 1st row, with the “+” and “–” signs of the terms alternating.

So, unlike a matrix, which is a table of numbers, a determinant is a number that is assigned to the matrix in a certain way.

Concept/definition of matrix. Types of matrices

Definition of a matrix. A matrix is ​​a rectangular table of numbers containing a certain number of m rows and a certain number of n columns.

Basic matrix concepts: The numbers m and n are called the orders of the matrix. If m=n, the matrix is ​​called square, and the number m=n is its order.

In what follows, the notation will be used to write the matrix: Although sometimes the notation is found in the literature: However, to briefly denote a matrix, one large letter of the Latin alphabet is often used (for example, A), or the symbol ||aij||, and sometimes with an explanation: A=||aij||=(aij) (i=1, 2,…,m; j=1,2,…n)

The numbers aij included in this matrix are called its elements. In the entry aij, the first index i is the row number, and the second index j is the column number.

For example, matrix this is a matrix of order 2×3, its elements are a11=1, a12=x, a13=3, a21=-2y, ...

So, we have introduced the definition of a matrix. Let us consider the types of matrices and give the corresponding definitions.

Types of matrices

Let us introduce the concept of matrices: square, diagonal, unit and zero.

Definition of a square matrix: Square matrix An n-th order matrix is ​​called an n×n matrix.

In the case of a square matrix The concept of main and secondary diagonals is introduced. The main diagonal of the matrix is called the diagonal going from the upper left corner of the matrix to its lower right corner. Side diagonal of the same matrix is ​​called the diagonal going from the lower left corner to the upper right corner. The concept of a diagonal matrix: Diagonal is a square matrix in which all elements outside the main diagonal are equal to zero. The concept of the identity matrix: Single(denoted E sometimes I) is called a diagonal matrix with ones on the main diagonal. The concept of a zero matrix: Null is a matrix whose elements are all zero. Two matrices A and B are said to be equal (A=B) if they are the same size (that is, they have the same number of rows and the same number of columns and their corresponding elements are equal). So, if then A=B, if a11=b11, a12=b12, a21=b21, a22=b22

This material was taken from the site highermath.ru

Matrices. Actions on matrices. Properties of operations on matrices. Types of matrices.

Matrices (and, accordingly, the mathematical section - matrix algebra) are important in applied mathematics, since they allow one to write down a significant part of mathematical models of objects and processes in a fairly simple form. The term "matrix" appeared in 1850. Matrices were first mentioned in ancient China, and later by Arab mathematicians.

Matrix A=A mn order m*n is called rectangular table of numbers containing m - rows and n - columns.

Matrix elements aij, for which i=j are called diagonal and form main diagonal.

For a square matrix (m=n), the main diagonal is formed by the elements a 11, a 22,..., a nn.

Matrix equality.

A=B, if the matrix orders A And B are the same and a ij =b ij (i=1,2,...,m; j=1,2,...,n)

Actions on matrices.

1. Matrix addition - element-wise operation

2. Subtraction of matrices - element-wise operation

3. The product of a matrix and a number is an element-wise operation

4. Multiplication A*B matrices according to the rule row to column(the number of columns of matrix A must be equal to the number of rows of matrix B)

A mk *B kn =C mn and each element with ij matrices Cmn is equal to the sum of the products of the elements of the i-th row of matrix A by the corresponding elements of the j-th column of matrix B, i.e.

Let us demonstrate the operation of matrix multiplication using an example

5. Exponentiation

m>1 is a positive integer. A is a square matrix (m=n) i.e. relevant only for square matrices

6. Transposing matrix A. The transposed matrix is ​​denoted by A T or A"

Rows and columns swapped

Example

Properties of operations on matrices

(A+B)+C=A+(B+C)

λ(A+B)=λA+λB

A(B+C)=AB+AC

(A+B)C=AC+BC

λ(AB)=(λA)B=A(λB)

A(BC)=(AB)C

(λA)"=λ(A)"

(A+B)"=A"+B"

(AB)"=B"A"

Types of matrices

1. Rectangular: m And n- arbitrary positive integers

2. Square: m=n

3. Matrix row: m=1. For example, (1 3 5 7) - in many practical problems such a matrix is ​​called a vector

4. Matrix column: n=1. For example

5. Diagonal matrix: m=n And a ij =0, If i≠j. For example

6. Identity matrix: m=n And

7. Zero matrix: a ij =0, i=1,2,...,m

j=1,2,...,n

8. Triangular matrix: all elements below the main diagonal are 0.

9. Symmetric matrix: m=n And a ij =a ji(i.e., equal elements are located in places symmetrical relative to the main diagonal), and therefore A"=A

For example,

10. Skew-symmetric matrix: m=n And a ij =-a ji(i.e., opposite elements are located in places symmetrical relative to the main diagonal). Consequently, there are zeros on the main diagonal (since when i=j we have a ii =-a ii)

Clear, A"=-A

11. Hermitian matrix: m=n And a ii =-ã ii (ã ji- complex - conjugate to a ji, i.e. If A=3+2i, then the complex conjugate Ã=3-2i)

Linear algebra

Matrices

Matrix size m x n is a rectangular table of numbers containing m rows and n columns. The numbers that make up a matrix are called matrix elements.

Matrices are usually denoted by capital Latin letters, and elements by the same, but lowercase letters with double indexing.

For example, consider a 2 x 3 matrix A:

This matrix has two rows (m = 2) and three columns (n ​​= 3), i.e. it consists of six elements a ij, where i is the row number, j is the column number. In this case, it takes values ​​from 1 to 2, and from one to three (written). Namely, a 11 = 3; a 12 = 0; a 13 = -1; a21 = 0; a 22 = 1.5; a 23 = 5.

Matrices A and B of the same size (m x n) are called equal, if they coincide element by element, i.e. a ij = b ij for , i.e. for any i and j (you can write "i, j").

Matrix-row is a matrix consisting of one row, and matrix-column is a matrix consisting of one column.

For example, is a row matrix, and .

Square matrix nth order is a matrix, the number of rows is equal to the number of columns and equal to n.

For example, a second-order square matrix.

Diagonal matrix elements are elements whose row number is equal to the column number (a ij, i = j). These elements form main diagonal matrices. In the previous example, the main diagonal is formed by the elements a 11 = 3 and a 22 = 5.

Diagonal matrix is a square matrix in which all non-diagonal elements are zero. For example, - diagonal matrix of third order. If all diagonal elements are equal to one, then the matrix is ​​called single(usually denoted by the letter E). For example, is a third-order identity matrix.

The matrix is ​​called null, if all its elements are equal to zero.

The square matrix is ​​called triangular, if all its elements below (or above) the main diagonal are equal to zero. For example, - triangular matrix of third order.

Operations on matrices

The following operations can be performed on matrices:

1. Multiplying a matrix by a number. The product of matrix A and number l is the matrix B = lA, whose elements b ij = la ij for any i and j.

For example, if , then .

2. Matrix addition. The sum of two matrices A and B of the same size m x n is the matrix C = A + B, the elements of which are with ij = a ij + b ij for "i, j.

For example, if That

.

Note that through the previous operations one can determine matrix subtraction same size: difference A-B= A + (-1)*B.

3. Matrix multiplication. The product of matrix A of size m x n by matrix B of size n x p is a matrix C, each element of which with ij is equal to the sum of the products of the elements of the i-th row of matrix A by the corresponding elements of the j-th column of matrix B, i.e. .

For example, if

, then the size of the product matrix will be 2 x 3, and it will look like:

In this case, matrix A is said to be consistent with matrix B.

Based on the multiplication operation for square matrices, the operation is defined exponentiation. The positive integer power A m (m > 1) of a square matrix A is the product of m matrices equal to A, i.e.

We emphasize that addition (subtraction) and multiplication of matrices are not defined for any two matrices, but only for those that satisfy certain requirements for their dimension. To find the sum or difference of matrices, their size must be the same. To find the product of matrices, the number of columns of the first of them must coincide with the number of rows of the second (such matrices are called agreed upon).

Let's consider some properties of the considered operations, similar to the properties of operations on numbers.

1) Commutative (commutative) law of addition:

A + B = B + A

2) Associative (combinative) law of addition:

(A + B) + C = A + (B + C)

3) Distributive (distributive) law of multiplication relative to addition:

l(A + B) = lA + lB

A (B + C) = AB + AC

(A + B) C = AC + BC

5) Associative (combinative) law of multiplication:

l(AB) = (lA)B = A(lB)

A(BC) = (AB)C

We emphasize that the commutative law of multiplication for matrices is NOT satisfied in the general case, i.e. AB¹BA. Moreover, the existence of AB does not necessarily imply the existence of BA (the matrices may not be consistent, and then their product is not defined at all, as in the above example of matrix multiplication). But even if both works exist, they are usually different.

In a particular case, the product of any square matrix A and an identity matrix of the same order has a commutative law, and this product is equal to A (multiplication by the identity matrix here is similar to multiplication by one when multiplying numbers):

AE = EA = A

Indeed,

Let us emphasize one more difference between matrix multiplication and number multiplication. A product of numbers can equal zero if and only if at least one of them equals zero. This cannot be said about matrices, i.e. the product of non-zero matrices can equal a zero matrix. For example,

Let us continue our consideration of operations on matrices.

4. Matrix Transpose represents the operation of transition from a matrix A of size m x n to a matrix A T of size n x m, in which the rows and columns are swapped:

%.

Properties of the transpose operation:

1) From the definition it follows that if the matrix is ​​transposed twice, we return to the original matrix: (A T) T = A.

2) The constant factor can be taken out of the transposition sign: (lA) T = lA T .

3) Transpose is distributive with respect to matrix multiplication and addition: (AB) T = B T A T and (A + B) T = B T + A T .

Matrix determinants

For each square matrix A, a number |A| is introduced, which is called determinant. Sometimes it is also designated by the letter D.

This concept is important for solving a number of practical problems. Let's define it through the calculation method.

For a first-order matrix A its determinant is its only element |A| = D 1 = a 11 .

For a second-order matrix A, its determinant is the number that is calculated using the formula |A| = D 2 = a 11 * a 22 – a 21 * a 12

For a third-order matrix A, its determinant is the number that is calculated using the formula

It represents an algebraic sum consisting of 6 terms, each of which contains exactly one element from each row and each column of the matrix. To remember the determinant formula, it is customary to use the so-called triangle rule or Sarrus rule (Figure 6.1).

In Figure 6.1, the diagram on the left shows how to select elements for terms with a plus sign - they are located on the main diagonal and at the vertices of isosceles triangles, the bases of which are parallel to it. The diagram on the left is used for terms with a minus sign; on it, instead of the main diagonal, the so-called side diagonal is taken.

Determinants of higher orders are calculated recurrently, i.e. a fourth-order determinant through a third-order determinant, a fifth-order determinant through a fourth-order determinant, etc. To describe this method, it is necessary to introduce the concepts of minor and algebraic complement of a matrix element (we immediately note that the method itself, which will be discussed below, is also suitable for third- and second-order determinants).

Minor M ij of element a ij of an n-th order matrix is ​​called the determinant of a (n-1)-th order matrix obtained from matrix A by deleting the i-th row and j-th column.

Every matrix of nth order has n 2 minors of (n-1)th order.

Algebraic complement A ij of an element and ij of a matrix of nth order is called its minor, taken with the sign (-1) (i+ j) :

A ij = (-1) (i+ j) *M ij

From the definition it follows that A ij = M ij if the sum of the row and column numbers is even, and A ij = -M ij if it is odd.

For example, if , That ; etc.

Determinant calculation method is as follows: the determinant of a square matrix is ​​equal to the sum of the products of the elements of any row (column) by their algebraic complements:

(expansion in elements of the i-th strings; );

(decomposition by elements of the j-th column; ).

For example,

Note that in the general case the determinant of a triangular matrix is ​​equal to the product of the elements of the main diagonal.

Let us formulate the basic properties of determinants.

1. If any row or column of the matrix consists of only zeros, then the determinant is equal to 0 (follows from the calculation method).

2. If all the elements of any row (column) of a matrix are multiplied by the same number, then its determinant will also be multiplied by this number (also follows from the calculation method - the common factor does not affect the calculation of algebraic additions, and all other terms are multiplied exactly this number).

Note: the sign of the determinant can be taken to be the common factor of a row or column (unlike a matrix, the sign of which can be taken to be the common factor of all its elements). For example, but .

3. When transposing a matrix, its determinant does not change: |A T | = |A| (we will not carry out the proof).

4. When two rows (columns) of a matrix are interchanged, its determinant changes sign to the opposite one.

To prove this property, first assume that two adjacent rows of the matrix are rearranged: the i-th and the (i+1)-th. To calculate the determinant of the original matrix, we perform an expansion in i-th line, and for the determinant of a new matrix (with rearranged rows) – by the (i+1)th (which is the same in it, i.e. coincides element-by-element). Then, when calculating the second determinant, each algebraic addition will have the opposite sign, since (-1) will not be raised to the power (i + j), but to the power (i + 1+ j), and otherwise the formulas will not differ. Thus, the sign of the determinant will change to the opposite.

Now suppose that not adjacent, but two arbitrary rows are rearranged, for example, i-th and (i+t)-th. Such a permutation can be represented as a sequential i-th offset lines are t lines down, and the (i+t)th line is (t-1) lines up. In this case, the sign of the determinant will change (t + t – 1) = 2t – 1 number of times, i.e. an odd number of times. Therefore, it will eventually reverse.

Similar reasoning can be changed for columns.

5. If a matrix contains two identical rows (columns), then its determinant is 0.

In fact, if identical rows (columns) are rearranged, then the same matrix with the same determinants will be obtained. On the other hand, according to the previous property, it must change sign, i.e. D = -D Û D = 0.

6. If the elements of two rows (columns) of the matrix are proportional, then the determinant is equal to 0.

This property is based on the previous property and bracketing the common factor (after bracketing the proportionality coefficient, there will be identical rows or columns in the matrix, and as a result this coefficient will be multiplied by zero).

7. The sum of the products of the elements of any row (column) of a matrix by the algebraic complements of the elements of another row (column) of the same matrix is ​​always equal to 0: for i ¹ j.

To prove this property, it is enough to replace the j-th row in matrix A with the i-th. The resulting matrix will have two identical rows, so its determinant is 0. On the other hand, it can be calculated by decomposing the elements of the jth row: .

8. The determinant of a matrix does not change if elements of another row (column) multiplied by the same number are added to the elements of a row or column of the matrix.

Indeed, let us add to the elements of the i-th row jth elements lines multiplied by l. Then the elements of the new i-th row will take the form
(a ik + la jk , "k). Let's calculate the determinant of the new matrix by decomposing the elements of the i-th row (note that the algebraic additions of its elements will not change):

We found that this determinant does not differ from the determinant of the original matrix.

9. The determinant of the product of matrices is equal to the product of their determinants: |AB| = |A| * |B| (we will not carry out the proof).

The properties of determinants discussed above are used to simplify their calculation. Usually they try to transform the matrix to such a form that any column or row contains as many zeros as possible. After this, the determinant can be easily found by expanding over this row or column.

inverse matrix

Matrix A -1 is called reverse in relation to a square matrix A, if when multiplying this matrix by matrix A both on the right and on the left, the identity matrix is ​​obtained: A -1 * A = A * A -1 = E.

From the definition it follows that the inverse matrix is ​​a square matrix of the same order as matrix A.

It can be noted that the concept of an inverse matrix is ​​similar to the concept of an inverse number (this is a number that, when multiplied by a given number, gives one: a*a -1 = a*(1/a) = 1).

All numbers except zero have reciprocals.

To solve the question of whether a square matrix has an inverse, it is necessary to find its determinant. If the determinant of a matrix is ​​zero, then such a matrix is ​​called degenerate, or special.

A necessary and sufficient condition for the existence of an inverse matrix: the inverse matrix exists and is unique if and only if the original matrix is ​​non-singular.

Let's prove the necessity. Let matrix A have an inverse matrix A -1, i.e. A -1 * A = E. Then |A -1 * A| = |A -1 | * |A| = |E| = 1. Therefore,
|A| No. 0.

Let's prove the sufficiency. To prove it, we simply need to describe a method for calculating the inverse matrix, which we can always apply to a non-singular matrix.

So let |A| ¹ 0. We transpose the matrix A. For each element A T we find an algebraic complement and compose a matrix from them, which is called annexed(mutual, allied): .

Let's find the product of the adjoint matrix and the original one. We get . Thus, matrix B is diagonal. On its main diagonal there are determinants of the original matrix, and all other elements are zeros:

Similarly, it can be shown that .

If you divide all the elements of the matrix by |A|, you will get the identity matrix E.

Thus , i.e. .

Let us prove the uniqueness of the inverse matrix. Suppose that there is another inverse matrix for A, different from A -1. Let's denote it X. Then A * X = E. Let's multiply both sides of the equality by A -1 on the left.

A -1 * A * X = A -1 * E

Uniqueness has been proven.

So, the algorithm for calculating the inverse matrix consists of the following steps:

1. Find the determinant of the matrix |A| . If |A| = 0, then matrix A is singular, and the inverse matrix cannot be found. If |A| ¹ 0, then go to the next step.

2. Construct the transposed matrix A T.

3. Find the algebraic complements of the elements of the transposed matrix and construct the adjoint matrix.

4. Calculate the inverse matrix by dividing the adjoint matrix by |A|.

5. You can check the correctness of the calculation of the inverse matrix in accordance with the definition: A -1 * A = A * A -1 = E.

1. Find the determinant of this matrix using the rule of triangles:

Let's skip the check.

The following properties of matrix inversion can be proven:

1) |A -1 | = 1/|A|

2) (A -1) -1 = A

3) (A m) -1 = (A -1) m

4) (AB) -1 = B -1 * A -1

5) (A -1) T = (A T) -1

Matrix rank

Minor kth order matrices A of size m x n is called the determinant of a square matrix of kth order, which is obtained from matrix A by deleting any rows and columns.

From the definition it follows that the order of the minor does not exceed the smaller of its sizes, i.e. k £ min (m; n). For example, from a 5x3 matrix A you can obtain square submatrices of the first, second and third orders (accordingly, calculate the minors of these orders).

Rank matrices are the highest order of the non-zero minors of this matrix (denoted by rank A, or r(A)).

From the definition it follows that

1) the rank of the matrix does not exceed the smaller of its dimensions, i.e.
r(A) £ min (m; n);

2) r(A) = 0 if and only if the matrix is ​​zero (all elements of the matrix are equal to zero), i.e. r(A) = 0 Û A = 0;

3) for a square matrix of the nth order r(A) = n if and only if this matrix A is non-singular, i.e. r(A) = n Û |A| No. 0.

In fact, to do this, it is enough to calculate only one such minor (the one obtained by crossing out the third column (because the rest will have a zero third column and are therefore equal to zero).

According to the triangle rule = 1*2*(-3) + 3*1*2 + 3*(-1)*4 – 4*2*2 – 1*(-1)*1 – 3*3*(-3) = -6 +6 – 12 – 16 + 1 +27 = 0.

Since all third-order minors are zero, r(A) £ 2. Since there is a non-zero second-order minor, for example,

Obviously, the methods we used (considering all kinds of minors) are not suitable for determining the rank in more complex cases due to their high complexity. Usually, to find the rank of a matrix, some transformations are used, which are called elementary:

1). Discarding null rows (columns).

2). Multiplying all elements of a row or column of a matrix by a number other than zero.

3). Changing the order of rows (columns) of a matrix.

4). Adding to each element of one row (column) the corresponding elements of another row (column), multiplied by any number.

5). Transposition.

If matrix A is obtained from matrix B by elementary transformations, then these matrices are called equivalent and denote A ~ B.

Theorem. Elementary matrix transformations do not change its rank.

The proof of the theorem follows from the properties of the determinant of the matrix. In fact, during these transformations the determinants of square matrices are either preserved or multiplied by a number that is not equal to zero. As a result, the highest order of non-zero minors of the original matrix remains the same, i.e. her rank does not change.

Using elementary transformations, the matrix is ​​brought to the so-called stepwise form (transformed into step matrix), i.e. they ensure that in the equivalent matrix there are only zero elements under the main diagonal, and non-zero elements on the main diagonal:

The rank of a step matrix is ​​equal to r, since by deleting columns from it, starting from the (r + 1)th and further, one can obtain a triangular matrix of rth order, the determinant of which will be non-zero, since it will be the product of non-zero elements (hence , there is a minor of rth order that is not equal to zero):

Example. Find the rank of a matrix

1). If a 11 = 0 (as in our case), then by rearranging the rows or columns we will ensure that a 11 ¹ 0. Here we swap the 1st and 2nd rows of the matrix:

2). Now a 11 ¹ 0. Using elementary transformations, we will ensure that all other elements in the first column are equal to zero. In the second line a 21 = 0. In the third line a 31 = -4. So that instead of (-4) there is 0, add to the third line the first line multiplied by 2 (i.e. by (-a 31 / a 11) = -(-4)/2 =
= 2). Similarly, to the fourth line we add the first line (multiplied by one, i.e. by (-a 41 /a 11) = -(-2)/2 = 1).

3). In the resulting matrix a 22 ¹ 0 (if a 22 = 0, then the rows could be rearranged again). Let’s ensure that there are also zeros below the diagonal in the second column. To do this, add the second line to the 3rd and 4th lines, multiplied by -3 ((-a 32 /a 22) = (-a 42 /a 22) = -(-3)/(-1) = - 3):

4). In the resulting matrix, the last two rows are zero, and they can be discarded:

A step matrix consisting of two rows is obtained. Therefore, r(A) = 2.